Egwald Mathematics: Geometry - 3D House

by

Elmer G. Wiens

Egwald's popular web pages are provided without cost to users.
Please show your support by joining Egwald Web Services as a Facebook Fan:
Follow Elmer Wiens on Twitter:

Painters and computer programmers struggle with perspective to depict 3-dimensional figures on a 2-dimensional surface. On this page you can view the house from different points-of-view, by changing three parameters, theta, phi, and rho. These three parameters are the spherical coordinates of the point P, the point-of-view of the observer. rho = distance from the origin to P theta = the angle between the x-axis and the projection           of the line from the origin to P onto the x-y plane phi = the angle from the z-axis to the point-of-view line
The three dimensional co-ordinate system consisting of the x, y, and z axis is drawn in black. The point-of-view of the observer, P, is drawn in blue. The perpendicular from P to the x-y plane, and the projection of P on the x-y plane, are in red.
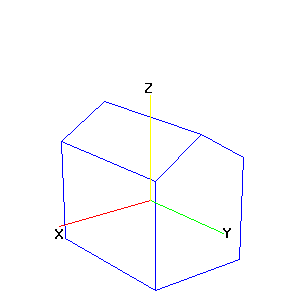
The house is displayed from the point-of-view of the observer. The x-axis (red), y-axis (green), and z-axis (yellow) spin with the house as the point-of-view changes.

Change the parameters, the angles are in radians, and click "Graph House" to view the house from a different perspective.